Sen(Qian)’s Memo

https://openreview.net/forum?id=NH29920YEmj

PUにMixupを導入する先行研究はいろいろあった。研究していくうちに、Negative Assumptionという識別器がPを予想以上に少なく判断する問題が起きている。

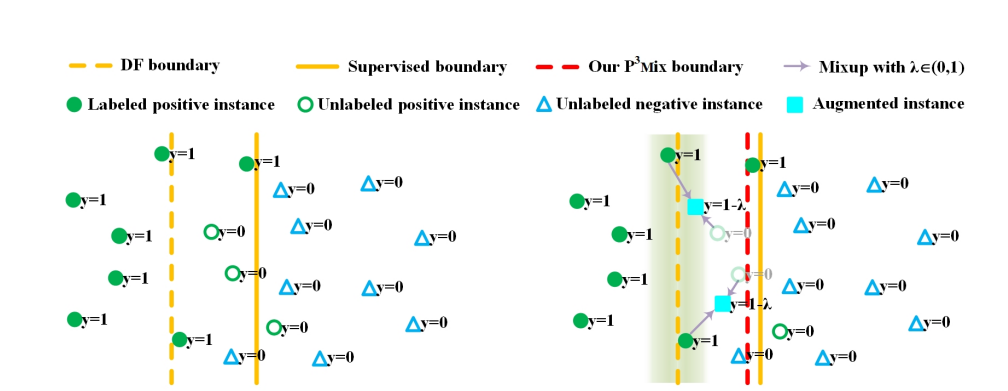
この研究では、上図のようにうまくmix-upする相手を選びつつdata augmentationをすることで、決定境界が過度にPをNに予測することを防ぐ。

識別境界の近くにある、Pっぽいけど実際Uとして扱われるのでcost-sensitiveでは重み付きのNとして扱われ、そしてその境界上のデータの存在は小さく扱われているのではないか、という仮説。

アイディアは、真の識別境界(実線)と偏ってしまったPUによる識別境界(点線)の間にある、実はPだがUになっているデータたちをPとすることができれば、Negative Assumptionを解決できないか？というもの。

MixUpを用いたPUは以下のような形をしているのが普通である。$\beta$は何かしらの重みを表す係数

P3Mixでは、以下のように修正する。Mixupしたデータで学習していく。

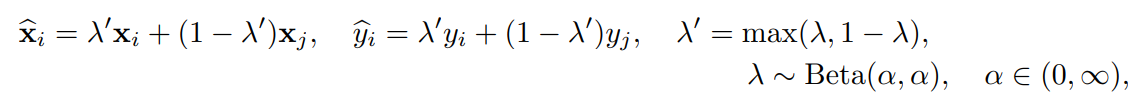
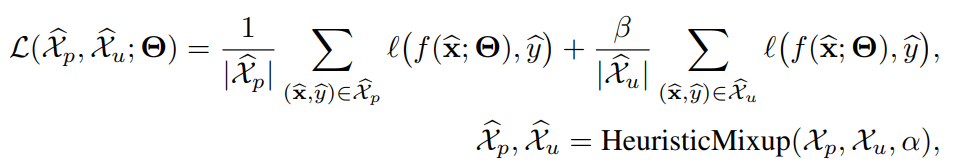
ここのheuristic mixupで妥当なmixupパートナーを見つけるという感じである。

先述のように、境界線付近のPデータはPU LearningさせるとNとして予測されがちであった。なので、現在の識別境界の近くにあるようなPデータ(PデータはPUで与えられるので)からmixupのプール$X_{cnd}$を作りたいよね。

具体的には、以下の方針でmixupする。

1. あるサンプル$\mathbf{x}_i, y_j$があるとする。
2. もし$\mathbf{x}_i$がUで($X_{cnd}$に入っておらず)、しかも識別境界の近くにある(これは後述の$X_{mpn}$に所属に該当)ならば、$X_{cnd}$から一様にmixup相手を選ぶ。
3. そうでないのならば、全体のサンプルから一様に選ぶ。

$f(g(\mathbf{x}))$は$f$がsigmoid関数で、$[0, 1]$にcalibrateした識別器だとする。

この時、識別境界の近くというのは、$\gamma \in [0.5, 1]$について、Uのデータ($y=0$はここでUという意味)かつ予測器の出力が、例えば$\gamma = 0.6$なら$0.4 \leq f(g(\mathbf{x})) \leq 0.6$の範囲にあるようなデータを曖昧なものとする。

距離ベースではなく。確率ベースで判断。

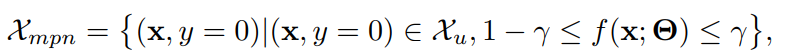
当然、識別境界の近くにあるといっても当然$X_{cnd}$に含まれない(そこに入っているのはPの中から選び出される)のが前提。

$X_P$の中から選び出す。

これは一定期間(毎エポックかな?)、$\mathbf{x} \in X_P$について、$f(g(\mathbf{x}))$の値について、Entropyを計算する。そして、Entropyが大きい方からtop-kで選ぶ。

すべてにおいて、

これだけでは学習が不安定になりがちなので、そこにさらにEarly-learning RegularizationとPseudo Negative Instance Calibrationする。

Early-learning Regularizationは学習の早期段階で以下のようなものをつける。つまり、学習の早期ではUはNegativeとしてみなしたうえで、Pの予測結果はPに近く、Uの予測結果はNの近くになるように仕向ける。

これを用いるにはP3Mix-Eというアルゴリズム。

Pseudo Negative Instanceは、Uの中でも先ほど使った$\gamma$によって、$f(g(\mathbf{x})) \geq \gamma$となるようなサンプルはほぼ確実にPだということで、今のイテレーション限定で、Pとして扱う。

これを用いるのはP3Mix-Cというもの。実験結果的にはこれは一番良かった。

OpenReviewに上がっているzipにあるコードを見る限り、どのP3Mixであっても

• 早い段階では、UをNとみなしてPN learningをしている。
• Mix-upした結果を最後にEntropy Minimizationをすることで、予測を偏らせることができる。

• FMNISTを使った。
  • Pは1, 4, 7でNはそれ以外。そしてNは1, 4, 7でPはそれ以外で実験。
• CIFAR10を使った。
  • Pは0, 1, 8, 9でNはそれ以外。そしてNは0, 1, 8, 9でPはそれ以外で実験。
• STL10を使った。
  • Pは0, 2, 3, 8, 9でNはそれ以外。そしてNは0, 2, 3, 8, 9でPはそれ以外で実験。

• nnPUにmixupを入れるより、この手法のほうがよかった
• だいたいの手法はGANベースのPANより良かったらしい。
• $\beta$(PとUのreweightingで使われる重みはハイパラ)は$\beta \geq 0.8$で安定するらしい。
• $\gamma$(境界線近くであるの判定)は$\gamma = 0.85, 0.9, 0.95$で安定するらしい。